Ian nepomniachtchi has been tired by playing all day long in the candidates tournament and in the same way, you must  be tired by reading my scholarly, educational articles. So let’s take a break and learn a fun fact called “Morphy Number“.

The Morphy number is a measure of how closely a chess player is connected to Paul Morphy (1837-1884) by way of playing chess games.

People who have played a chess game with Morphy have a Morphy number of 1. Players who did not play Morphy but played someone with a Morphy number of 1 have a Morphy number of 2. People who played someone with a Morphy number of 2 have a Morphy number of 3, et cetera.

Morphy number 1

Morphy is known to have played about 100 people, but all of the known links for players with Morphy number 2 go through the following five players. A few years after the early lists of players were tabulated, it was discovered that Mortimer (pictured down below) was Morphy’s friend and he played casual games with him, so is Morphy Number 1, so previous lists needed to be drastically revised to promote many players. This is because Mortimer had a very long, if not particularly successful, career, including the Ostende-B 1907 tournament. This enabled many famous younger players to gain Morphy Number 2. These include Mieses, Tartakower, Znosko-Borovsky, and Bernstein, who played beyond WW2, enabling still younger players to become Morphy Number 3. Some Irish players could go through the Rev. Dr George Salmon, who played in one of Morphy’s blindfold chess simultaneous exhibitions. So the five main players are:-

• Adolf Anderssen
• Henry Bird
• James Mortimer
• John Owen
• Louis Paulsen

Morphy number 2

Everyone in this group played someone in the group above. The Australian champion Frederick Esling (pictured down below) achieved Morphy Number 2 by beating Anderssen in an offhand game and another Australian champion, Julius Leigh Jacobsen (1862-1916) achieved Morphy Number 2 by beating Bird in a casual match enabling many Australian players of the early 20th century to achieve Morphy Number 3. The following are some of the most important players who have achieved Morphy Number 2:-

• Aron Nimzowitsch
• Harry Pillsbury
• Akiba Rubinstein
• Emanuel Lasker
• Mikhail Chigorin
• David Janowski
• Carl Schlechter
• Frank James Marshall
• Siegbert Tarrasch
• Wilhelm Steinitz

Morphy number 3

Most of the masters in this group played several members of the previous group. This group includes some of the most important players for making connections to later generations. Botvinnik and Reshevsky (pictured down below) played older masters such as Lasker and Janowski, had long careers, and played many younger players. Najdorf was Tartakower’s pupil and they played a number of published games together, and Najdorf played blitz right into his 80s, allowing many younger players to achieve 4. Smyslov and Keres had very long careers, so much younger players achieved Morphy Number 4 by playing them. Gligoric also played Tartakover, allowing many Yugoslav players to achieve Morphy Number 4. C.J.S. Purdy played Tartakower, enabling many Australian players to achieve Morphy Number 4. Fairhurst, who played Tartakover, was many times champion of Scotland, and later moved to New Zealand, so a number of players in these countries achieved Morphy Number 4 by playing him.

• Max Euwe
• Svetozar Gligoric
• Reuben Fine
• Miguel Najdorf
• Samuel Reshevsky
• Rudolf Spielmann
• Bent Larsen
• José Raúl Capablanca
• David Bronstein
• Pal Benko
• Mikhail Botvinnik
• Edward Lasker

Morphy number 4

And this is many of the players we now know today. Since many people already had Morphy number 3 from various countries, most of the top-tier grandmasters undoubtedly have Morphy Number 4. The list includes:-

• Viswanathan Anand
• Donald Byrne
• Bobby Fischer
• Mark Dvoretsky
• Vassily Ivanchuk
• Anatoly Karpov
• Garry Kasparov
• Viktor Korchnoi
• Susan Polgar
• Judit Polgar
• Tigran Petrosian
• Lev Polugaevsky
• Yasser Seirawan
• Alexei Shirov
• Boris Spassky
• Peter Svidler[
• Mikhail Tal
• Mark Taimanov
• Veselin Topalov

However, I do not want to end the article on this note. I would like to present to you an interesting problem regarding Morphy’s Number. If you’re not even close to a computer science specialist or do not have an interest at it, the article is over. You can start reading my next articles. However, if you are a mathematician or computer science specialists reading this, then you can proceed ahead. If you still don’t understand, make sure to read the article again to get a review on what we have covered. Alternatively, you can read about the Erdos number for mathematicians or the Bacon number for actors. It is merely the same idea presented but in a different context.

Q) What is the most efficient way to find out a certain players morphy number?

Warning: This is about to get really messy from here. It’s advisable to leave.

Approach 1

You’d have to find a list of players Morphy has played. Then, you’d research as many players who played each of those players. This can all be done by searching by player in a large database. Eventually you’d have a large tree, and the problem comes down to an optimal search algorithm.

You’d search “branches” with a more likely chance of giving you a small Morphy number. This means looking at players who have played more games over their career. For example, if some player A was one of Morphy’s opponents who played the most games, you’d look at him first. Then, find one of Player A’s opponents (call him B) who played the most games in his lifetime, and look at him first. If doing this recursively with B never leads to you (or gives a poor Morphy number), go on to C: the opponent of player A who played the second most games. If eventually you find all of Player A’s opponents don’t lead to you, meaning Player A isn’t connected to you, go on to the opponent of Morphy who had the second most games.

But it’s still a massive job to search and although solves the problem but doesn’t tick the box of being the most efficient way. Even if you find a link to yourself, you need to prove/justify that it’s the smallest link. Perhaps you could organize all these players into a tree and write a program to efficiently search it.
This is the simple approach and would be the first one that comes to mind. But I was more interested in Approach 2, so let’s look at it now.

Approach 2

In computer science, this is a solved problem. For example, you can use Dijkstra’s algorithm. You can read it’s wikipedia page here. What is described here looks like a depth-first algorithm. There is an easy, intuitive breadth-first algorithm: Take all players directs connected to Morphy. They form set 1. Then, take the set of all players directly connected to set 1. That’s set 2. You add layers of sets until you find yourself or there is no further layer. That in fact gives you all the shortest paths from Morphy to anyone. This can be computed very efficiently as well because these set operations are fast.

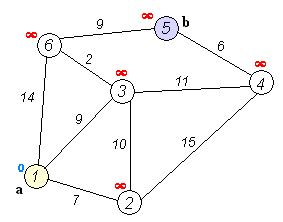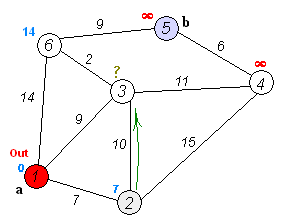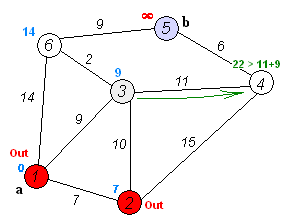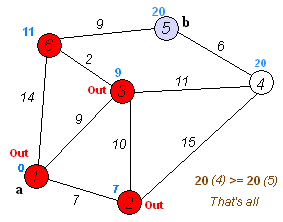
With Approach 1, you can define a useful distance heuristic so that more likely paths are searched first probably with heuristic on time or geography? With this approach, you can precompute all answers and store them. 1 million players and 100 million games could be processed completely in a few seconds. This is also NOT exponential. Essentially, the set based method perform a “flood fill” starting from Morphy. It’s like flood fill in MS Paint. Once a pixel has been visited/colored there is no need to look at it again. The number of possible paths is exponential but they are not all visited because the search stops at already colored pixels. The graph has at most one node for every chess player in the database, and for each node, it has at most as many links as the number of different opponents a player can meet in a lifetime (which can be estimated to be 100). So it can’t grow any larger than 100 million links. And for this reason Dijkstra’s algorithm is much better than depth-first search for finding shortest paths in large graphs.

And since, the chess community mostly overlaps with geeks and nerds (which is not a bad thing!), I thought I’d give a non-chess related question. If you’ve found both approaches, give yourself a pat on the back. This was pretty tough so here’s your reward. A cool Dijkstra’s algorithm meme.

Note: The second approach was recommended to me by my friend studying computer science at CMU. Due to personal reasons, I will not mention his name here. But honestly, I didn’t even know Dijkstra’s algorithm and thought of the intuitive first method approach. So don’t worry if you couldn’t get it at first try, we’re in the same boat 🙁

What’s your Morphy Number? Comment it down below. I will be reading all of the comments for this article.

Happy Learning,

Yash Mehta